
“立体拼合”实用技巧
1.题型判定
提问:题干中完整图形是由残缺图形与哪个选项共同构成?
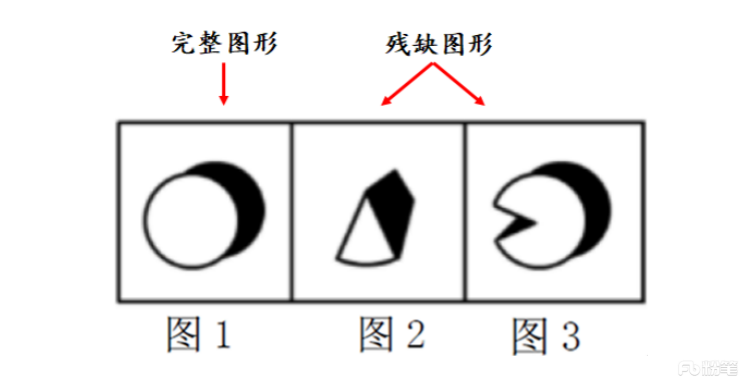
题干:给出一个完整图形及几个残缺图形(如下图所示)。
2.解题思路
凹凸一致,有凹必有凸,有凸必有凹。具体要考虑两个方面:
(1)凹进去的部分与凸出来的部分形状相同,如上图中图2与图3可拼合为图1。
(2)凹进去的部分与凸出来的部分对应长度相同。
粉笔小贴士:
立体拼合题目可以先观察题干和选项的“凹凸”部分的形状,通常情况下可以排除1-2个错误选项,再对剩余选项拼合的部分进行长度上的比较。
例题1
下图中的立体图形①是由立体图形②,③和④组合而成,下列哪一项不能填入问号处?
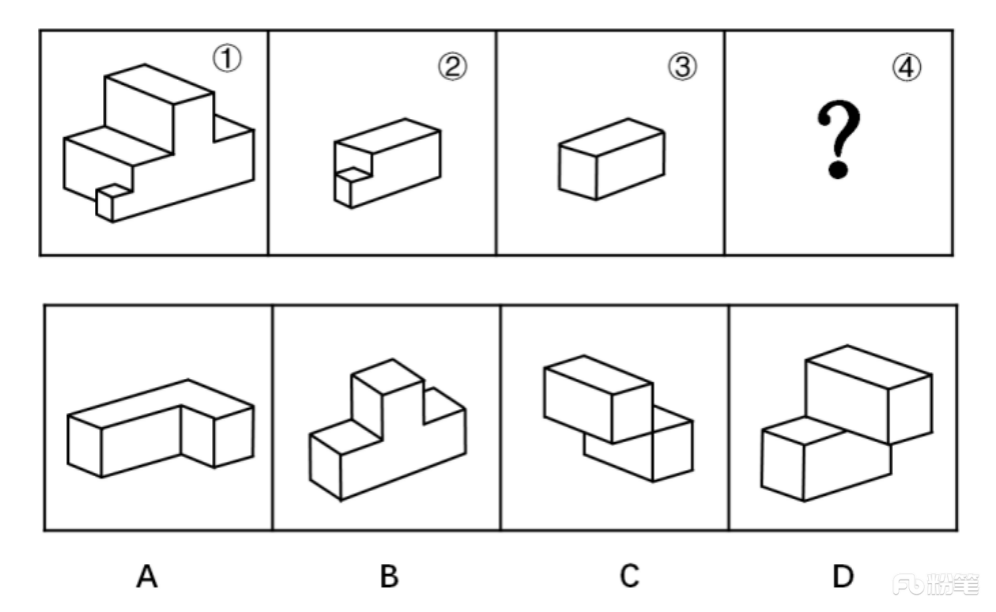
【题型判定】通过问题可直接判断题型为立体拼合,即图形②③④可以拼合成图形①。
【题目分析】本题考查立体拼合。题干中①为整体,②③④组合后构成①,其中A、C、D选项均能与②③组合构成①,具体组合方式如下所示:

本题为选非题,故正确答案为B。
粉笔小贴士:
立体拼合题目无需观察整体是否可以拼合,只需观察图形特殊的“凹凸”的部分,同时要多利用排除法做题。
例题2
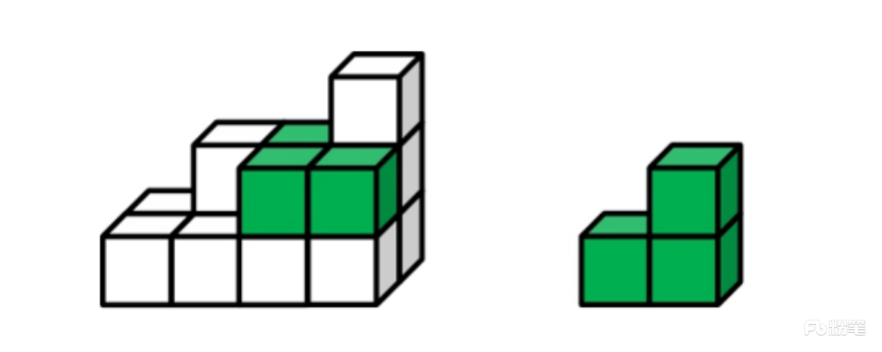
下列哪个选项可与①和②组成一个长方体?

【题型判定】通过问题可判定本题考查立体拼合,即题干和其中一个选项拼合成一个完整的长方体。
【题目分析】此题为立体图形拼接问题,做题原则为凹凸一致。首先根据题干可知组成的是一个8*3的长方体,图①有3层,11个小方块,且最下面一层不缺方块,图②有3个小方块,可知要找一个有2层,10个小方块的图形,B项有13个小方块,C项有3层,排除B、C两项。从下向上逐层分析题干图形,第一层放了8个小方块,在第二层中把图②插进图①里,如下图所示,则第二层还差3个小方块,且3个小方块呈“L”形,排除A项。
故正确答案为D。
粉笔小贴士:
1.小方块立体拼合的题目近年来频繁出现,是命题的趋势,如果选项小方块数量不同,可先根据小方块的数量进行排除。
2.当选项图形与题干残缺图形无法满足“凹凸一致”的原则时,可尝试将题干图形或选项图形进行简单的旋转与翻转,再利用“凹凸一致”原则进行验证。
“截面图”必会技巧
1.题型判定:
提问:题干中给出一个立体图形,问哪项能够(或不能)成为其截面。
题干:给出一个立体图形,通常会具体描述立体图形的形状。
例题
一立方体如图所示从中挖掉一个圆锥体,然后从任意面剖开,下面哪一项不可能是该立方体的截面:

解析:
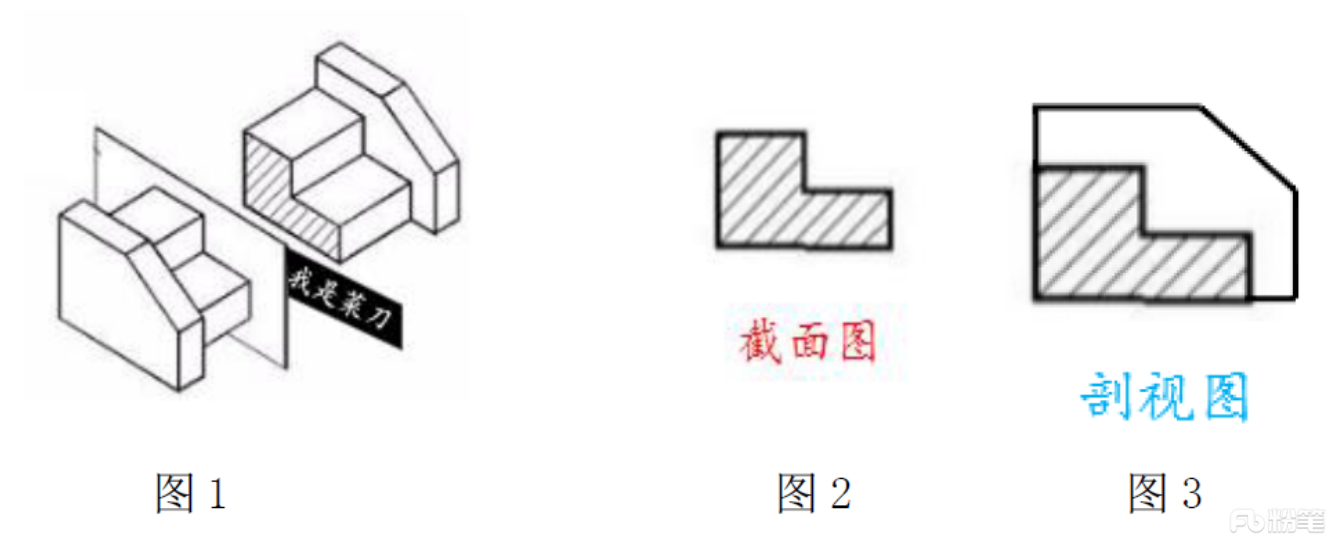
截面图-指的是被切部分的形状。
剖视图-假想用一个剖切平面将物体剖开,移去介于观察者和剖切平面之间的部分,对于剩余部分向投影面所做的正投影图。
粉笔小贴士:
截面图与剖视图的区别要重点掌握,大多的考试题目考查的都是截面图,剖视图常作为迷惑项出现。
2.解题思维
(1)解题原则:一刀切。①一刀切到底;②不能拐弯。
(2)常见立体图形截面(以最常见的六面体、圆柱、圆锥、圆台等基础图形为例)
截面图给出的立体图形一般是基础图形的组合(如立方体+圆锥),因此掌握常见立体图形的截面是做题的基础。
①六面体
a.矩形(拦腰切、上下切、斜切)
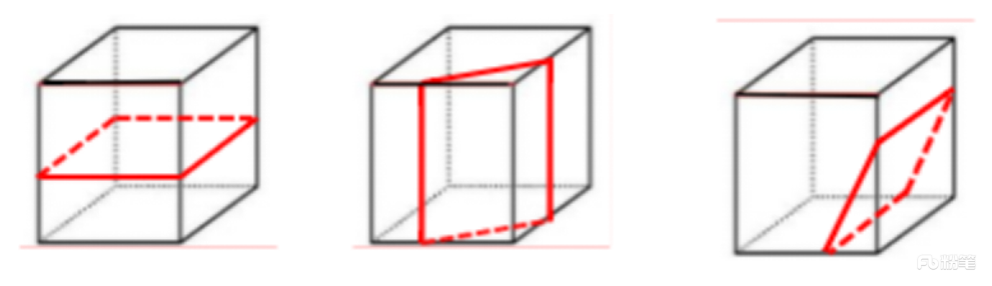
b.梯形(斜切)

c.三角形(从棱上的某一点开始斜着切到面)

需要注意,六面体只能切出锐角三角形,无法切出直角、钝角三角形。
②圆柱

a.圆(横切);b.椭圆(斜切);c.矩形(竖切)
③圆锥
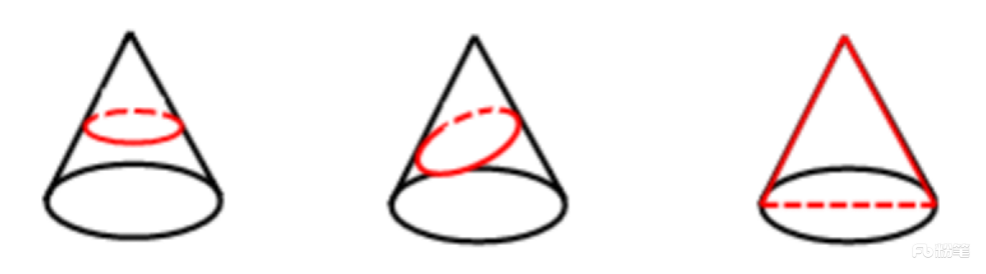
a.圆(横切);b.椭圆(斜切);c.三角形(竖切过顶点)
④圆台
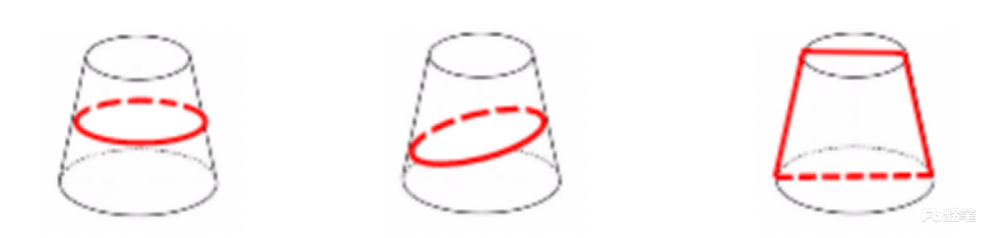
a.圆(横切);b.椭圆(斜切);c.梯形(竖切)
粉笔小贴士:
1.题目中选项图形的切割方向主要集中在横切、竖切和斜切上,因此要掌握基础图形沿这三种方向所切出的图形形状。
2.圆柱、圆锥、圆台横着切均是“圆”,斜着切均是“椭圆”。需要特别注意的是圆柱从上向下斜着切两侧是曲线,而不是直线。
例题1
左边为给定的立体图形,从任意角度剖开,右边哪一项是它的截面图?
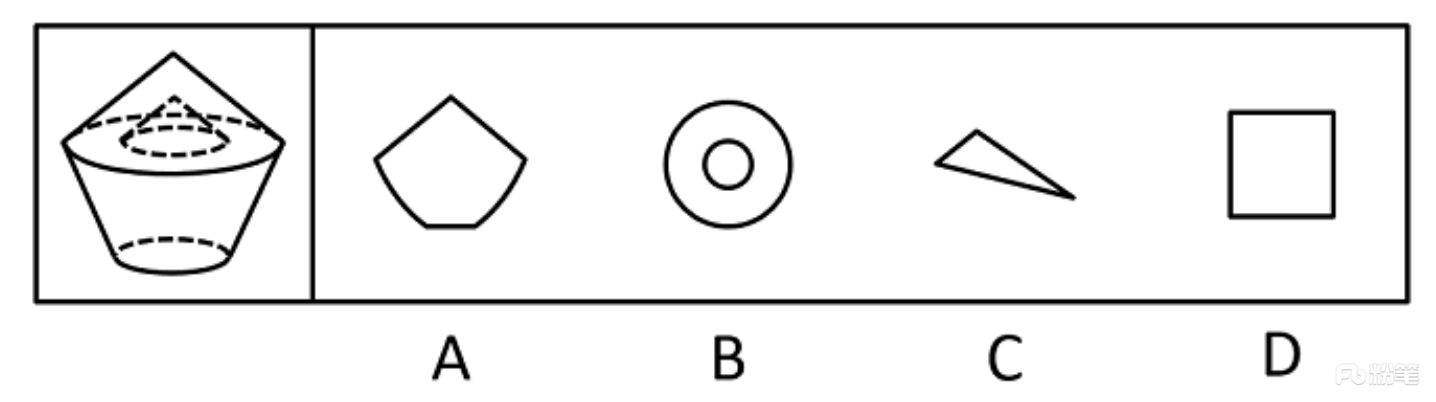
【题型判定】通过问题可以判断本题考查截面图,要求选出的是截面的选项。
【题目分析】本题考查截面图,逐一分析选项。
A项:下半部分从上向下切出的应该是梯形,选项与题干不一致,排除;
B项:如下图所示,从图形上半部分横着切,经过中间空心部分即可得到,当选;
C项:无法切出,排除;
D项:无法切出,排除。
故正确答案为B。
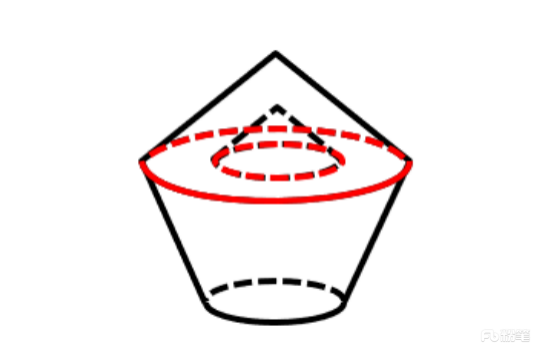
例题2
下列选项中,不属于左侧立体图形的截面的是:

【题型判定】通过问题可以判断本题考查截面图,要求选出的是“不属于左侧立体图形的截面的”,即不能成为截面的选项。
【题目分析】本题考查截面图,逐一分析选项。

A项:无法切出,当选;
B项:如图所示,从图形正上方切入,垂直向下切即可得到,排除;
C项:如图所示,从图形下方切入,平行于底面切即可得到,排除;
D项:如图所示,从图形中间切入,平行于底面切即可得到,排除。
本题为选非题,故正确答案为A。
粉笔小贴士:
1.截面题题目问题多要求选择“不可能”的截面选项;
2.当整体无法判断图形的截面图时,可分解成基础图形进行判断;
3.熟练掌握常见的六面体、圆柱、圆锥、圆台等基础图形的各种截面形状。
“三视图”做题思路
1.题型判定:
提问:从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:
题干:给出立体图形以及它的三个三视图(如下图所示)。

立体图形的三视图分为主视图(从正面看)、俯视图(从头顶向下看)以及左视图(从左侧看),如下图所示:
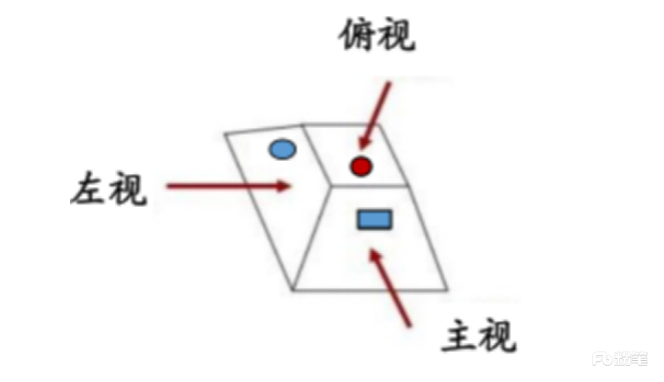

上图中,图(1)为左视图,图(2)为主视图,图(3)为俯视图。
粉笔小贴士:
三视图题目的提问方法虽然与图形推理中平面规律的提问方法相同,但题干图形的特征较为明显,通常会出现一个立体图形和两个三视图。
实际做题中,出题人不一定会严格按照左视、俯视、主视的角度来考查,可能出现右视图(从右向左)和仰视图(从下向上)等,要具体情况具体分析。
2.解题思维
(1)所有的三视图都是平面图。若选项中出现立体图形,则一定错误。
(2)原图有线就有线,原图没线就没线。
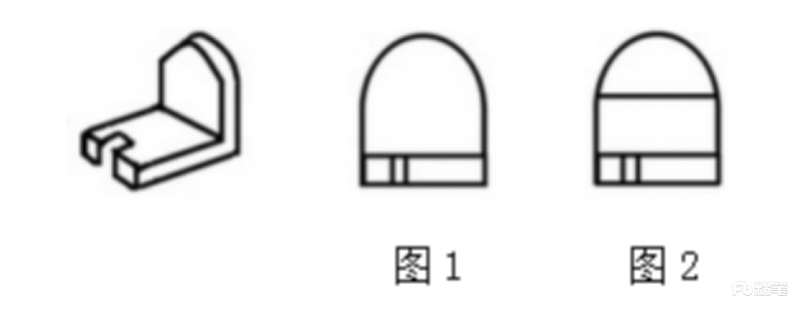
如上图所示,图1和图2都是立体图形从左前方往右后方观察的,立体图形上方内部明显无横线,所以三视图也应无横线,图1正确,图2错误。
(3)当被遮挡住时,看不见被遮挡部分。

如上图所示,图1、图2以及图3都是从立体图形左前方往右后方观察的,需要分两种情况进行讨论:①若只有图1和图2,得出的应是图1,因为后面的矩形应被前方的图形遮挡,被遮挡的部分应用虚线表示;②若只有图2和图3,得出的应是图3,被遮挡的部分用虚线表示最严谨,若没有用虚线表示,则遮挡的部分应不画出来。
(4)有些角度下弧会被压平。
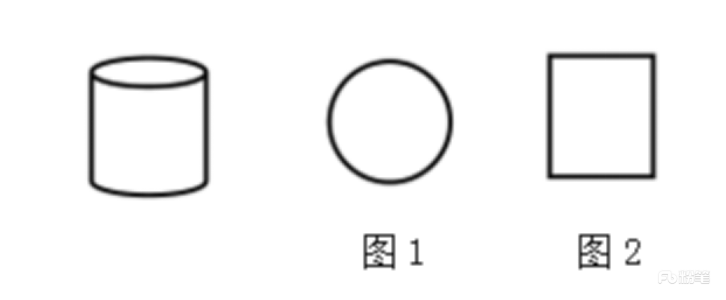
如上图所示,图1是圆柱体的俯视图,图2是圆柱体的主视图、左视图以及右视图。
粉笔小贴士:
三视图中被遮挡的部分是否应画虚线,需要从题干已知图形进行判断,与题干已知图形保持一致即可。
当立体图形出现曲线时,要注意当观察角度(视线的方向)与曲线在同一水平线时,则观察到的应是直线。
例题1
下列选项不可能是左侧立体图形视图的是( )。

【题型判定】通过题目问题可直接判定本题考查三视图。
【题目分析】本题考查三视图。
A项:从后往前看可以得出,为后视图,排除;
B项:从任意角度看都无法得出此图形,当选;
C项:从前往后看可以得出,为主视图,排除;
D项:从左往右看可以得出,为左视图,排除。
本题为选非题,故正确答案为B。
例题2
左图为给定的多面体,从任一角度观看,右边哪项可能是该多面体的视图?

【题型判定】通过题目问题可直接判定本题考查三视图。
【题目分析】本题考查三视图,逐一分析选项。
A项:从下往上看,题干A选项右上角应为梯形,排除; 如下图所示
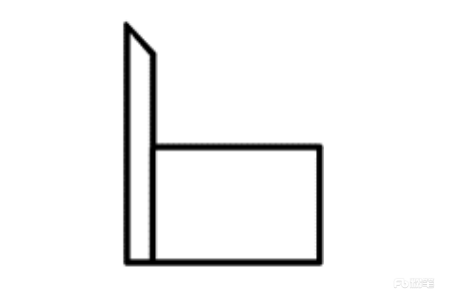
B项:从前往后看,与题干一致,当选;
C项:从上往下看,题干C选项左下角应为梯形而非长方形,排除;如下图所示
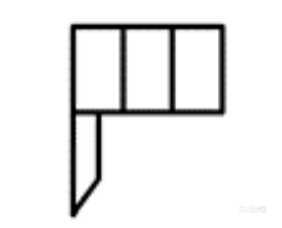
D项:从右往左看,题干D选项右下角应为长方形而非梯形,排除。如下图所示
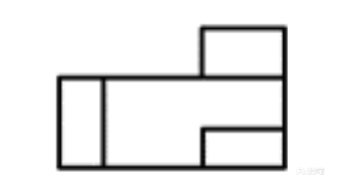
故正确答案为B。
粉笔总结:
立体拼合、截面图与三视图三种题型的考试内容相对固定,立体拼合题目要遵循“凹凸一致”的解题原则,遇到小方块的拼合题目,当选项小方块数不同时,优先考虑小方块数;截面图除了要掌握截面图与剖面的区别,更要掌握“一刀切”的解题原则,最重要的是常见基础图形的截面形状,即使是难题也可以转换成基础图形再去研究;三视图要了解解题的思路,尤其是立体图形出现遮挡和曲线时,要注意细节的判断。
最后,希望同学们能通过学习,掌握好立体拼合、截面图以及三视图的做题方法和技巧,在备考过程中不断练习,攻克难点,在考场中顺利得分!