策略制定
行测小讲堂
计数问题
（一）题型特征：
问多少种情况 / 多少种可能 / 多少种方式 / 多少个。
（二）解题方法：
情况数较少时，枚举法，不重复不漏掉，建议有大数字到小数字依次枚举。
情况数较多时，排列组合，分步相乘、分步相加，有顺序用A、没有顺序用C。
在进行实际解题时，核心在于梳理，整合和分类。要将题干的信息进行简化梳理，让关系更明确;然后将梳理之后的题干条件进行进一步的整合和分类，之后就可以按照整合和分类的信息解决问题。
例题演练
（2022四川）有一批数量足够多且长度分为3、4、5、6、7厘米的细钢条，从中适当选取3根钢条作为三角形的三条边，则可能围成（ ）个不同的三角形。
A.25
B.28
C.30
D.32
【思路梳理】
根据题意，需要围成三角形，则所选三根钢条应满足任意两边之和大于第三边，任意两边之差小于第三边，可根据围成的三角形形状进行分类讨论。
【解题步骤】
①等边三角形，可构成边长分别为3、4、5、6、7的等边三角形，共5个不同的三角形；
②等腰三角形：以3厘米为腰的等腰三角形只有3、3、4和3、3、5两种，其余以4、5、6、7厘米为腰的等腰三角形均有四种，则一共可构成2+4×4=18个不同的三角形；
③一般三角形，其中边长为3、4、7厘米的不能构成三角形，则一共有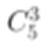
-1=（5×4×3）/（3×2×1）-1=9个不同的三角形。
综上所述，共有5+18+9=32个。
故正确答案为D。